What does a good math programme look like?

The Ford government hasn’t come up with anything yet to fill in the mathematical hole it says was created by “discovery learning”. So, School Magazine would like to clarify a few basics.

What does a solid math program look like?  The 2005 Ontario Mathematics Curriculum tries to provide a start. It’s not nearly specific enough, but does note that learning should be related to what students already know and can apply to other topics. The curriculum says that learning should be meaningful, involve concrete materials – counters, balls, items from the store and so on – that make abstract math concepts more approachable. It tells teachers to use math across the curriculum: “in Grade 6 concepts associated with the fulcrum of a lever can be used to develop a better understanding of the impact that changing a set of data can have on the mean.” In grade 2 students could be “given the opportunity to relate the study of location and movement in the Geometry and Spatial Sense strand of mathematics to the study of movement in the Structures and Mechanism Strand in science and technology.”

That may not help most people understand what makes a good mathematics program, so here are some features we think are important:

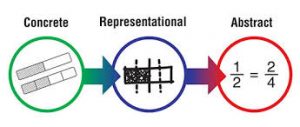
• Teachers need to consider three steps for teaching a new concept in mathematics: the concrete step, the representational step and then the abstract step. Let’s say a teacher wants to get across the idea that 1/2 and 2/4 mean the same thing. He would have students work with blocks divided up into halves and quarters and get students to compare them – the concrete step. The next  – representational- step would be to give have divide pictures into halves and quarters.  Finally, the abstract step would show:       1/2 = 2/4

 

• Math must be tied to everyday experiences of students. Some students, might estimate the cost of items they buy at the grocery store, then figure out how much change they get. Others could calculate the area of a room to carpet and apply the square metre cost to come up with a price. Grade 7 students could use what they know about percentage to decide whether or not a book that costs $18.49 should really have a total price, including tax, of $22.37 – or whether they’re getting conned. It’s all practical.

 

• Students need to be able to transfer what they’ve learned in math to other topics and vice versa. For instance, in grade 3 students learn to compare lengths like centimetres, metres and kilometres. It’s just good standard teaching practice to apply them to lengths of body parts, distance from school to home, the length of the school hallway and so on.

 

• Patterns are critical for learning math – seeing how, changing one thing affects everything else. In grade 5 students are shown that by adding the same number to other numbers (12+5; 17 +5; 22+5; 27 +5 …) creates a pattern.

• Certain skills need to be automatic – counting by different numbers like 5s, and 10s adding and subtracting groups of numbers. But being automatic goes beyond that. In grade 6 students are taught what it means to rotate something like a car, 90 or 180 degrees. Patterns like these should be applied easily by students. This aspect of learning also includes what is called “mental math strategies” like making change from a purchase.

 

• Discovery is fine, but it needs to be guided. This is clear in the TDSB’s outline which tells teacher to use “play, exploration, investigation, direct instruction and practice.” It’s not a matter of leaving it up to the kids to find out how to do math, teachers use different methods to suit different students and situations.

• To that end good math teaching revolves around solving a problem. For instance, in Grade 8, students might be asked to work on this problem as they learn about proportions: “The ratio of stone to sand in HardFast Concrete is 2 to 3. How much stone is needed if 15 bags of sand are used?”

 

• Teaching needs to be done in small steps. A student is not going to understand a concept like proportion in one go. It’s all about breaking this abstract idea into bite-sized pieces children can relate to. How much a teacher has to break down a large concept depends very much on a particular classroom at a particular time.

 

• Along with this, teachers need to be aware of their students’ learning zones. If math tasks are easy for children, they can practice and make their skills more automatic, and increase confidence. But they aren’t learning anything new. If math tasks are in their zone the learn something new with instruction from the teacher and can link it to what they already know. For example, in grade 3, students are expected to work out equations like 25-4 = 15+ __. The zone for learning is not going to start with that problem. It’s going to be where students understand that the equation breaks down to 21= 15 + __.

 

• Students should not be scared off math. See “small steps” above. If teachers can make math make sense, tie it to what students know, provide the amount of guidance needed and break concepts down into small enough steps, math might just become a series of little victories rather than one large phobia. Confidence cuts through everything in learning.

 

• Assessment of learning needs to be varied, long term and ongoing. It should not be about passing a test like the one set by EQAO (Education, Quality and Accountability Office) for students in grades 3, 6 and 9. Teachers need to promptly assess whether or not groups of their students understand what they’ve been taught so they adjust their teaching, adding more directed instruction or practice.

These are just some of the more important features of a solid math programme. Each of these can break down into smaller parts. Both Toronto District School Board and Ministry of Education guides spend a lot of time on diverse learning styles, language, ethnic and gender backgrounds, use of games and many other aspects of math learning.

All of this underlines the need to prioritize what is taught from the Ontario Mathematics Curriculum. Whatever the Ford government decides to do in order to introduce more rigor or toughen things up in math, it’s nothing but a show if the Ministry can’t identify – in light of all its apparent priorities about diversity, practical understanding and centering learning on children – what really must be taught.

Finally, whatever Mr. Ford decides to do about math, he will never know how well students are learning if his government relies on large scale assessments like EQAO. It’s far better to assess students individually or in small groups so that the person doing the assessment can judge where a child is having difficulty with a concept or even if it is math that poses the problem and not the way the question is written. Collect information from all the small assessments and you have a sample of student knowledge that can give a much better picture of mathematics skills across the province. A large-scale assessment is too blunt a tool to dig out how well kids are learning math.

It just doesn’t add up.